Mathematics of the etheric
Just as solid matter and its behaviour is described with a certain type of mathematics and laws, different forces and worlds are bound by different laws and require a different language [see 1921-06-GA205 references below]. This is because the language chosen by science for describing the mineral aspects of physical matter is very much fitted to the characteristics of what is described. However, the nature of other dimensions of nature is quite different, and the language or mathematical representation of mineral science breaks down, or is just not fitted to do this.
The Spectrum of elements and ethers, and Formative forces require such different kind of mathematics. In mineral matter centric forces are at work, causing solid substance, gravity and weight. The formative forces in the etheric are characterized by different properties of expansion and contraction and are peripheral (between the point and the plane) rather than centric.
Contemporary physics, as foundation for Mineral science, is based on Euclidean geometrical thinking of space measured in finite and rigid lengths, with areas and volumes based on the measurement of length, with laws of parallelism and the right angle. The implicit underlying assumption being that this applies from the smallest to the largest dimensions. And as any frame of reference, it limits what we can see or describe in the frame. In this case the thinking of space is very much earthly, meaning related to our human sensory experience of vision and confirmation by tactile experience.
See also: Top five problems with current science
From the study of perspective in the middle ages arose a new kind of geometry that includes not just the finite forms but also the infinite space: vanishing lines and points of perspective. In that new geometry the infinitely distant is treated realistically, a bold step in thought.
Reasoning with this other geometry, complementary to the long-established Euclidean geometry, has two implications:
- focus is no longer on rigid fixed forms such as square or circle, but on mobile types of form that change depending on perspective or geometric transformation. Hence a conic section can result in a circle, ellipse, parabola, hyperbola. It is a foundational concept for qualitative spatial thinking about the metamorphoses of living form.
- principle of duality or polarity: projective geometry recognizes as the deepest law of spatial structure an underlying polarity which can be called, in simple and imaginative language, the polarity of expansion and contraction. Expansion and contraction of a sphere leads to two limits of a point or a plane. In other words: three-dimensional space can equally well be formed from the plane inward as from the point onward. These two polar opposite aspects represent the essence of spatial structure. Its implication is that whatever geometrical form or law is conceived, there will always be a sister form or law in which roles of point and plane are interchanged.
Now if these points are taken together, we start to think of universal space as
- a) not just pointwise but also planar (perspective outside in instead inside out) and
- b) with a balanced relation between contractive and expansive, or centric and peripheral qualities.
Aspects
- Counterspace terminology
- Note the concept of 'counter-earth', referring to counterspace (see mathematical framework), already appears in Pythagoras (Antichthon), and also Aristotle described it. According to Aristotle the function of the Counter-Earth was to explain "eclipses of the moon and their frequency". See also: Threefold Sun
Illustrations
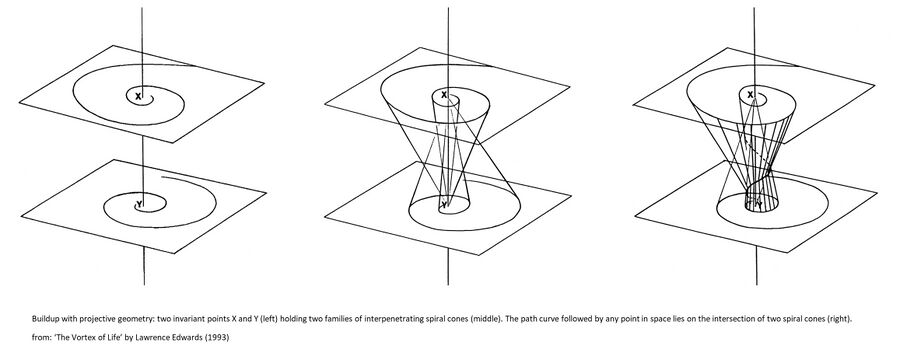
Schema FMC00.674: shows the principle of applied projective geometry as a mathematical basis for the laws that give form to organic and plant life in nature through the etheric formative forces. More specifically this illustrates the concept of calculating a 'path curve' of points in space, that lie on the intersection of two interpenetrating spiral cones from two invariant points. For more info, see Mathematics of the etheric
As shown in the reference work 'The Vortex of Life’ by Lawrence Edwards (1993), computer simulations render quite exactly the measured forms of buds of flowers, but also the form of the human heart, thereby corresponding to qualitative descriptions by Rudolf Steiner (see Schema FMC00.675).
Lecture coverage and references
19th century innovative thinking
Nick Thomas refers to the mathematicians Janos Boyai (1802-1860) and Nikolai Lobatchevsky (1792-1856) who were first to prove the fact that there can be other types of geometry than the one we learn about at school, each established a different possibility: either that space is closed or is 'more open than open'. In fact it seems Carl Friedrich Gauss (1777-1855) already discovered this fact 40 years earlier, but did not dare to publish it. However this line of thinking was not welcomed in a science fully engrained in Euclidean geometrical thinking.
Synthetic or 'projective geometry' was developed around 1820-1840 by French mathematicians Jean-Victor Poncelet (1788-1867), Joseph Gergonne (1771-1859) and Michel Chasles (1793-1880) and independently by the Swiss Jakob Steiner (a pupil of Pestalozzi) (1796-1863).
Later, around 1871 the concept of path curves or W-curves was developed by the friends and collegues Felix Klein (1849-1925) and Sophus Lie (1842-1899).
Rudolf Steiner's indications
Rudolf Steiner already mentioned non-Euclidean geometry for study of the etheric and as a way out of the mineral scientific worldview in 1910. The term of 'counterspace' and the idea of 'peripheral forces' (re centripetal & centrifugal) and 'suction', was introduced by Rudolf Steiner in the lectures of 1920-03-11-GA321 (where he introduces this for the first time), re-iterating it in and calling it 'counter-space' in 1920-05-02-GA201 and elaborating it further in the 1921-01-GA323 lectures.
To position, see also: Four kinds of lawfullness in 1921-06-24-GA205 and 1921-06-24-GA205
Reference extracts
1921-01-15-GA323
20th century progress
Projective geometry and path curves were taken up further by mathematicians George Adams Kaufmann (1894-1963) and Louis Locher-Ernst (1906-1962), and this work was continued by Lawrence Edwards (1912-2004) and Nick C. Thomas (1941-2015).
Adams, Edwards and Thomas were instrumental in integrating the mathematical framework with the spiritual scientific foundations for a meta-representation whereby current mineral science is expanded with a science to explain phenomena of life based on the etheric formative forces.
Various
1880 - Dostoevsky
in 'Brothers Karamazov'
.. there have been and still are geometricians and philosophers, and even some of the most distinguished, who doubt whether the whole universe, or to speak more widely the whole of being, was only created in Euclid's geometry; they even dare to dream that two parallel lines, which according to Euclid can never meet on Earth, may meet somewhere in infinity. I have come to the conclusion that, since I can't understand even that, I can't expect to understand about God. I acknowledge humbly that I have no faculty for settling such questions. I have a Euclidian earthly mind, and how could I solve problems that are not of this world? And I advise you never to think about it either, my dear Alyosha, especially about God, whether He exists or not. All such questions are utterly inappropriate for a mind created with an idea of only three dimensions.
Discussion
Note 1 - Inversion research
Paul Schatz (1898-1979) was a German-born sculptor, inventor and mathematician who studied the inversion of the platonic solids. Schatz is most known for his discovery of the new 'oloid' shape in 1929.
Inversion is a dynamic metamorphosis process by which a form turns inside out, interchanging its inner and outer surfaces. Using mobile models of the Platonic solids, Schatz demonstrated that the cube can undergo projective inversion: its faces tip through six joints to form a hollow frame before returning to the original solid in a continuous, cyclical movement. He extended this principle to all regular polyhedra, laying the foundations for what became known as Platonic inversion.
Schatz not only developed the Invertible Cube with its specific rhythmic mobility but also found an additional movement consisting of a rhythmically pulsing inversion that was added to the two basic movements of rotation (rotary motion) and translation (translational motion in a straight line). This new type of motion is the basis for novel technical designs and applications.
One such application is fluid mixers [such as developed by the company Oloid AG in CH (1993), continuted by Hortimax BV in NL (2007) and Inversions-Technik GmbH in CH (2012) - see link below]. The oloid shape unwinds 100% of its surface during inversion and this is a lever for highly efficient movement of liquids: oloids can be can be used to homogenize large quantities of liquids using relatively low energies (e.g. up to 10,000 m³ of water can be mixed with just 220 W).
Further reading and references
- Paul Schatz foundation website
- Oloid based technology and applications: www.oloid.de/en/oloid-technology/origin-of-the-oloid-geometry/
Note 2 - Use of computing to graphically simulate the etheric formative forces
General introduction on mathematics by computer
Computers have opened a new horizon for mankind also because they allow to program simple formulas and mini-program, and let the formula be calculated forward, or the mini-program be processed, thus providing dynamic sequences both graphical and in time.
This has enabled the visualization of the emergence of form as we know it in nature. Examples are Benoit Mandelbrot's M-series that gives rise to fractals and fractal geometry, or to a lesser extent similarly Stephen Wolfram's idea of using cellular automata.
The merit of such approaches in the new area of 'mathematics by computing' is that an obvious link appears with forms in nature, due to the dynamics of the algorithms computed. However mostly we are left with nice visuals, and we can stand in awe, but that is where it currently ends.
However to avoid any misunderstandings, these models are not used on projective geometry as laid out on this topic page, they are merely the initial discoveries that show this new dimension, without having tuned in to the right frequency to link it to the laws of nature itself.
Using the computer for explaining form in nature
What really should be done is to connect into this approach the 'Mathematics of the etheric', to apply this principle of adding the growth-over-time dimension by using the graphical simulation power of the computer.
For some first (early and rather basic) examples, see: Overview on etheric research and the plant kingdom#Computational mathematics
Various links
- Mandelbrot set
- for an introduction see ao documentary 'The Colours of Infinity' (1995), here on youtube. The documentary nicely explains
- https://en.wikipedia.org/wiki/Fractal#Natural_phenomena_with_fractal_features
Related pages
- Formative forces
- Spectrum of elements and ethers
- Scientific research into the etheric formative forces
- Overview on etheric research and the plant kingdom
- Lemniscatory timespace
References and further reading
- Wassily Kandinsky: Point, line and plane (1926, 1979)
- Louis Locher-Ernst (1906-1962)
- Space and Counter-Space, in DE as 'Raum und Gegenraum'
- Urphänomene der Geometrie (1980)
- Projektive Geometrie (1980)
- George Adams
- Strahlende Weltgestaltung : synthetische Geometrie in geisteswissenschaftlicher Beleuchtung, zugleich als Vorarbeit gedacht für eine geistgemässe mathematische Physik
- Physical and ethereal spaces (1965, based on essay 1933)
- Grundfragen der Naturwissenschaft : Aufsätze zu einer Wissenschaft des Ätherischen
- The lemniscatory ruled surfaces in space and counterspace
- Von dem ätherischen Raume (1964)
- Universalkräfte in der Mechanik : Perspektiven einer anthroposophisch erweiterten mathematischen Physik
- Universalkräfte in der Mechanik : Vektoren in Raum und Gegenraum ; Urraumschrauben
- Frank Ayres: Projective geometry (1967)
- Olive Whicher: 'Projective geometry' (1970)
- Nick Thomas
- Science between space and counterspace (1999)
- Space and counterspace: a new science of gravity, time and light (2008)
- Oliver Conradt: 'Mathematical Physics in Space and Counterspace'
- Henrike Holdrege: 'To the Infinite and Back Again - A Workbook in Projective Geometry'
- For another example of contemporary work on projective geometry, see eg the work of Charles G. Gunn (profile)